Nombre: Yomara Estefania Castillo Tomala
Unidades:
Una unidad de medida es una cantidad estandarizada de una determinada magnitud física. En general, una unidad de medida toma su valor a partir de un patrón o de una composición de otras unidades definidas previamente. Las primeras unidades se conocen como unidades básicas o de base (fundamentales), mientras que las segundas se llaman unidades derivadas. Un conjunto de unidades de medida en el que ninguna magnitud tenga más de una unidad asociada es denominado sistema de unidades.
Todas las unidades denotan cantidades escalares. En el caso de las magnitudes vectoriales, se interpreta que cada Lo Ji de los componentes está expresado en la unidad indicada.
El Sistema Internacional de Unidades es la forma actual del sistema métrico decimal y establece las unidades que deben ser utilizadas internacionalmente. Fue creado por el Comité Internacional de Pesos y Medidas con sede en Francia. En él se establecen 7 magnitudes fundamentales, con los patrones para medirlas:
1. Longitud
2. Masa
3. Tiempo
4. Intensidad eléctrica
5. Temperatura
6. Intensidad luminosa
7. Cantidad de sustancia

SISTEMA INTERNACIONAL DE UNIDADES DE MEDIDA (S.I.)
El Sistema Internacional de Unidades, abreviado S.I., también denominado Sistema Internacional de Medidas, es el heredero del antiguo sistema métrico decimal, por lo que el S.I. también es conocido de forma genérica como sistema métrico.
Una de las principales características del Sistema Internacional de Medidas es que sus unidades están basadas en fenómenos físicos fundamentales. Las unidades del S.I. son la referencia internacional de las indicaciones de todos los instrumentos de medida, y a las que están referidas a través de una cadena ininterrumpida de calibraciones o comparaciones.
El Sistema Internacional de Unidades consta de siete unidades básicas, también denominadas unidades fundamentales, que definen a las correspondientes magnitudes físicas fundamentales, que han sido elegidas por convención, y que permiten expresar cualquier magnitud física en términos o como combinación de ellas. Las magnitudes físicas fundamentales se complementan con dos magnitudes físicas más, denominadas suplementarias.
Por combinación de las unidades básicas se obtienen las demás unidades, denominadas unidades derivadas del Sistema Internacional, y que permiten definir a cualquier magnitud física.
En la siguiente Tabla se puede seleccionar cualquier magnitud física para acceder a definiciones, sus unidades de medida expresadas en el S.I. y su equivalencia con otros sistemas de medida.
— TABLA DE MAGNITUDES FÍSICAS —
Sistema Internacional de Unidades de Medida (SI)
MAGNITUDES FÍSICAS FUNDAMENTALES
Longitud
Unidad Básica Sistema Internacional (S.I.): metro (m)
Definición: Un metro (m) se define, según la Conferencia General de Pesas y Medidas, al fijar el valor numérico de la velocidad de la luz en el vacío, c, en 299 792 458, cuando se expresa en la unidad m·s-1, donde el segundo se define en función de la frecuencia del cesio 133, ΔνCs.
De la relación exacta c = 299 792 458 m·s-1 se obtiene la siguiente expresión para el metro, expresada en función de las constantes c y ΔνCs :
Resultado de esta definición es que el metro es la longitud del trayecto recorrido por la luz en el vacío durante un intervalo de tiempo de 1/299 792 458 de segundo.
Equivalencias
1 Amstrong (Å) = 10-10 m
1 nanómetro (nm) = 10-9 m
1 Thou (thou) = 2,54 x 10-5 m
1 píxel (px) = 0,000264583 m (0,264583 mm)
1 pulgada (inch, in) = 0,0254 m (25,4 mm)
1 pie (foot, ft) = 12 in = 0,3048 m
1 yarda (yard, yd) = 3 ft = 36 in = 0,9144 m
1 rod = 1 perch = 5,5 yd = 5,0292 m
1 milla (mile, mi) = 1609,34 m
1 milla marina = 1852 m
1 braza = 1,83 m
1 legua = 4828,03 m
1 Año luz = 9,46 x 10
Masa
Unidad Básica Sistema Internacional (S.I.): kilogramo (kg)
Definición: El kilogramo (kg) se define al fijar el valor numérico de la constante de Planck, h, en 6,626 070 15 × 10-34, cuando se expresa en la unidad J·s, igual a kg·m2·s-1, donde el metro y el segundo se definen en función de c y ΔνCs .
De la relación exacta h = 6,626 070 15 × 10-34 kg·m2·s-1 se obtiene la unidad kg·m2·s-1, y de ésta la expresión para el kilogramo en función del valor de la constante de Planck h :
De aquí, junto con las definiciones del segundo y el metro, se obtiene la definición de la unidad de masa en función de las tres constantes h, ΔνCs y c :
A resultas de esta definición queda definida la unidad kg·m2·s-1 (la unidad de las magnitudes físicas acción y momento angular). Junto con las definiciones del segundo y del metro, esto conduce a la definición de la unidad de masa en función del valor de la constante de Planck, h.
Anteriormente, para definir el kilogramo como la unidad de masa del S.I. se hacía referencia a un determinado patrón existente. De esta manera, se definía al kilogramo como la masa igual a la de un cilindro de 39 milímetros de diámetro y de altura, de una aleación de 90% de platino y 10% de iridio, que está ubicado en la Oficina Internacional de Pesos y Medidas, en Sèvres, Francia.
Equivalencias:
1 onza (ounce, oz) = 0,02834952 kg
1 libra (pound, lb) = 0,4535924 kg
1 tonelada métrica (t) = 1000 kg
1 tonelada corta (ton short, tn) = 907,1847 kg
1 tonelada larga (long) = 1016,047 kg
1 gramo (g) = 1,0000·10-3 kg
1 arroba (a) = 11,5 kg
1 stone (st) = 6,350293 kg
1 quintal métrico = 100 kg
1 quintal corto estadounidense (Short hundredweight) = 45,359237 kg
1 quintal largo británico (Long hundredweight) = 50,80234544 kg
1 dracma avoirdupois = 1,7718451953125 g
1 dracma troy = 3,8879346 g
1 grano (gr) = 0,06479891 g
Unidad Básica Sistema Internacional (S.I.): segundo (s)
Definición: El segundo (s) se define al fijar el valor numérico de la frecuencia de la transición hiperfina del estado fundamental no perturbado del átomo de cesio 133, ΔνCs , en 9 192 631 770, cuando se expresa en la unidad Hz, igual a s-1.
De la relación exacta ΔνCs = 9 192 631 770 s-1 se obtiene la expresión para la unidad segundo, en función del valor de ΔνCs :
Como resultado de esta definición, el segundo también se puede definir como la duración de 9 192 631 770 períodos de la radiación correspondiente a la transición entre los dos niveles hiperfinos del estado fundamental no perturbado del átomo de cesio 133, a una temperatura de 0 K.
https://youtu.be/nqxHnu4LJ6k
Aquí tenemos un vídeo explicativo
Las unidades atómicas
forman un sistema de unidades conveniente para la física atómica, electromagnetismo, mecánica y electrodinámica cuánticas, especialmente cuando nos interesamos en las propiedades de los electrones. Hay dos tipos diferentes de unidades atómicas, denominadas unidades atómicas de Hartree y unidades atómicas de Rydberg, que difieren en la elección de la unidad de masa y carga. En este artículo trataremos sobre las unidades atómicas de Hartree. En au, los valores numéricos de las siguientes seis constantes físicas se definen como la unidad:
Dos propiedades del electrón, la masa y carga;
Dos propiedades del átomo de hidrógeno, el radio de Bohr y el valor absoluto de la energía potencial eléctrica en el estado fundamental;
Dos constantes, la constante de Planck reducida o constante de Dirac y la constante de la ley de Coulomb.
Aquí tenemos un ejemplo :
Dimensiones de una magnitud
Independientemente de la unidad que se emplee para expresar una magnitud física, estas se clasifican en tipos diferentes, según en la forma que puedan sumarse. Por ejemplo, podemos sumar una distancia de 3 km con una de 2 millas, o podemos sumar 5 kg a 3 libras, pero sabemos que es erróneo sumar 3 km con 5 kg. Vemos que hay algo más básico que la unidad de medida y es el tipo de magnitud de que se trata: distancia, masa, tiempo,… A cada uno de estos tipos se denomina dimensión y decimos que una magnitud tiene “dimensiones de distancia” o “dimensiones de masa”.
1.3 Homogeneidad dimensional
Para clasificar las magnitudes tenemos el principio de homogeneidad dimensional que establece que:
En toda ecuación y en toda suma, los términos igualados o sumados deben tener las mismas dimensiones.
Ésta es una forma elegante de decir “no se pueden sumar peras con manzanas”. Este principio constituye una herramienta extremadamente útil para detectar errores en los cálculos. Imaginemos que como resultado de un problema se llega a que una fuerza es igual a
F = A(r-r^2)\,
siendo r un radio y A una constante. Esta ecuación es necesariamente incorrecta, sin necesidad de sustituir valor numérico alguno. Estamos sumando una distancia, r, (que tiene dimensiones de longitud) con una distancia al cuadrado (que sería un área). Puesto que estas cantidades poseen dimensiones diferentes, la ecuación no es válida.
Aquí tenemos otro ejemplo de ecuación dimensionalmente incorrecta:
Archivo:newcuyama.jpg
La homogeneidad dimensional permite localizar de forma rápida errores en los resultados de un problema.
Una relación entre magnitudes no implica ninguna unidad en concreto (solo las dimensiones). Al decir que la distancia Sevilla y Cádiz es la misma que entre Sevilla y Huelva, da igual que la midamos en kilómetros o en pulgadas. Por ello, es incorrecto escribir una ley como
E = \frac{1}{2}mv^2\,(\mathrm{julios}) (expresión incorrecta)
ya que la energía podría estar expresada en ergios, calorías, kilovatios·hora o muchas otras, dependiendo de en qué midamos la masa o la velocidad. Por ello, la regla es que si una fórmula es puramente algebraica, no hay que incluir las unidades. Por contra, si se sustituyen uno o todos los valores numéricos, es obligatorio incluir las unidades.
1.4 Ecuaciones dimensionales
Aunque magnitudes diferentes no se pueden sumar, si se pueden multiplicar. Podemos dividir una magnitud con dimensiones de distancia por una con dimensiones de tiempo y obtenemos una magnitud con dimensiones de velocidad. Escribimos esta relación
[v] = \frac{[x]}{[t]}
donde el corchete representa “dimensiones”. Debemos insistir en que esta ecuación no nos dice que la velocidad sea igual al espacio partido por el tiempo, sino que sus unidades son las de una distancia dividida por un tiempo (que pueden ser m/s o km/h, por ejemplo).
La homogeneidad dimensional nos permite determinar las dimensiones de cantidades desconocidas. Así, en la ley de Hooke
F = -kx\,
nos dice que la constante k tiene dimensiones de fuerza partida por distancia
[k]=\frac{[F]}{[x]}
(por ejemplo, se medirá en N/m).
La existencia de relaciones entre dimensiones permite dividir las magnitudes en fundamentales y derivadas. De una relación como
S = b\cdot h\,
obtenemos que las dimensiones de área son las de una distancia al cuadrado, lo que podemos escribir como
[b] = L\qquad\qquad [h] = L\qquad\Rightarrow\qquad [S] = L^2
De esta forma, las dimensiones de cualquier magnitud se puede expresar como potencias de una serie de magnitudes fundamentales.
Así, por ejemplo, la velocidad equivale al cociente de una distancia dividida por un intervalo de tiempo y por tanto se verifica la ecuación dimensional
[v] = \frac{[x]}{[t]} = L T^{-1}
Aquí la distancia y el tiempo son consideradas magnitudes fundamentales y la velocidad una magnitud derivada.
Las magnitudes que se eligen como fundamentales e incluso el número de ellas es arbitrario. En el SI existen siete magnitudes fundamentales: longitud, tiempo, masa, intensidad de corriente eléctrica, cantidad de materia, temperatura termodinámica e intensidad luminosa. Todas las demás son derivadas.
Cada magnitud derivada posee una única ecuación dimensional, caracterizada por los diferentes exponentes de las magnitudes fundamentales.
Magnitud Relación Dimensiones
Área [S] = [x]2 L^2\,
Volumen [V] = [x]3 L^3\,
Velocidad [v] = [x] / [t] L\,T^{-1}\,
Aceleración [a] = [v] / [t] L\,T^{-2}\,
Fuerza [F] = [m][a] M\,L\,T^{-2}\,
Trabajo [W] = [F][x] M\,L^2T^{-2}\,
Potencia [P] = [W] / [t] M\,L^2T^{-3}\,
Teniendo las ecuaciones dimensionales de las diferentes magnitudes que aparecen en una ecuación, podemos establecer de forma sistemática si es dimensionalmente correcta.
Así, por ejemplo, la ecuación para una velocidad de impacto con el suelo
v = \sqrt{2gh}
con h la altura inicial, v la velocidad de impacto y g la aceleración de la gravedad
Hay que repetir que la homogeneidad es independiente de las unidades que se empleen para medir las cantidades. Por lo que sabemos, h podría estar medido en leguas, y v en micras/semana. Las dimensiones de una magnitud son algo más básico que las unidades en que se midan.
https://youtu.be/H27dO9Qi82I
Aquí hay un vídeo que nos detalla

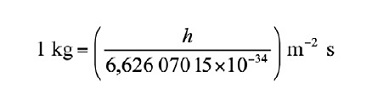
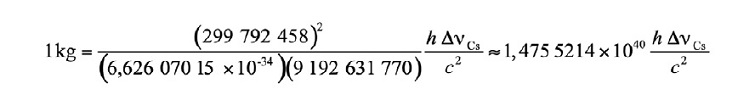
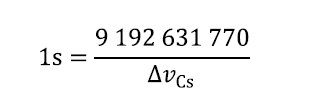






Comentarios
Publicar un comentario